ДВОЙСТВЕННОСТЬ.

"Главная и первая из наук - это наука о зарождении понятий "чет" и "нечет" и том значении, которое они имеют по отношению к природе вещей". Платон, Послезаконие. 1.

1. Двойственность. Предмет исследования.

Как это не покажется странным, но ни в одном философском словаре или философской энциклопедии вы не найдете статьи, посвященной понятию - "двойственность". Это тем более странно, что двойственные понятия широко используются в философии и различных отраслях специального знания ( в физике, математике, химии и др.). Однако, до сих пор не было сделано попытки систематизировать с учетом достижений современной науки все то, что "действительно удивительно и божественно для вдумчивого мыслителя - это присущее всей природе удвоение числовых значений, и наоборот, раздвоение-отношение, наблюдаемое во всех видах и родах вещей" (Платон, 1999).

Конечной целью такого рассмотрения, которая, конечно, выходит за рамки данной статьи, является попытка создать связную, логичную и необходимую систему общих идей, объединенных понятием "двойственность", в терминах которых можно было бы интерпретировать каждый элемент нашего опыта.

Такое исследование, на наш взгляд, должно во-первых, выделить двойственность как предмет специального изучения, сформулировать сновные положения, раскрывающие сущность двойственности и характер ее движения, и во-вторых, обозначить контуры всеобщей теории двойственности, показать всю методологическую мощь и эвристическую ценность, заключенную в двойственном подходе.

Двойственность многолика и изменчива, и в этом, пожалуй, одна из трудностей в ее описании. Дуализм, диада, дихотомия, бинарная оппозиция, противоположность, полярность - вот, наверное, еще не полный перечень понятий, затрагивающих в тех или иных аспектах сущность двойственности. Не вдаваясь пока в тонкости различных дефиниций и их отношения, "сцепления" с двойственностью, отметим, что в принципе возможно было бы отказаться от старого термина -"двойственность" и создать новый, но мы не пошли этим путем, так как новые значения старых слов не устраняют их старых значений, а скорее обогащают их¹. Также постоянная трудность рассуждений с использованием двойственности заключается в том, что необходимо "растягивать" мысль и ее вербальное выражение за пределы обычного унарного употребления. Мысля о чем то, мы концентрируем свое внимание на том, о чем мыслим, и вынуждены игнорировать все, не относящееся к делу. Но в любом рассмотрении отдельного факта присутствует в качестве скрытой предпосылки его координация с окружением, которое требуется для его существования. Поэтому, модальность мысли преодолевается в обыденной жизни употреблением выражений типа "с одной стороны", "с другой стороны", а в философии этот путь размышления был назван Гегелем удвоением явления: "Мы таким образом удваиваем явление, ломая его надвое: на внутреннее и внешнее, на силу и проявление, на причину и следствие" (Гегель, 1998).

2.Двойственность. Представления древних.

Идея двойственности - очень старая идея, которая дошла до нас в различных мифах древних народов. Геб и Нут у египтян, Ки и Ан у шумеров, Пракрити и Пуруша у индийцев, Инь и Янь у китайцев, Ометикутль и Омесигуатль у ацтеков, Ахриман и Ормюзд у персов-все это названия богов или активных двойственных начал, взаимодействие которых, по мнению древних, приводит в движение мир. Эти дуальности (так мы для удобства будем называть стороны двойственности) вступают в союз, где их различия теряются, образуя целое, обладающее способностью к движению, развитию. Так, Пракрити и Пуруша объединяются в Прадхане, Янь и Инь сливаются в Дао, Ахраман и Ормюзд соединяются в Митре, Ометеотль образует единое для Ометикутля и Омесигуатля. Общая идея, заключенная в этих древних теориях в различных вариантах сводится примерно к следующему. Источник мира лежит в проявлении порядка внутри бесформенного основания-хаоса. Как только порядок устанавливается из хаоса, тогда начинают проявляться различные структуры и картины мира. Действительная порождающая сила, которая лежит в основе различных проявлений мира может быть найдена во внешних движениях двойственности. Эта двойственность порождена в первичном порядке как акт чистого различения из которого появляются двойные принципы: небеса и земля, день и ночь, мужской и женский. В то время, когда дуальности объединены в союз, они имеют неопределенную (потенциальную в смысле возможности к свершению) энергию. Но разделенные как чистые полярности, после погружения в бесформенное основание, обладающее неограниченной энергией источника, эта неопределенная энергия преобразуется в активный потенциал, который способен произвести изменения. Собственно, уже в этом описании ( воспроизводится в основном по Питу (Peat, 1987)) содержатся элементы современных теорий ( порядок, хаос, дифференциация, поток, колебания, связность и др.), которые как мы увидим, имеют прямое отношение к двойственности. Можно только удивляться прозорливости и интуиции древних мыслителей, идеи которых через толщу тысячелетий дошли до нас, чтобы вновь получить развитие на пути интеграции различных наук на основе принципа двойственности.

3. Двойственность. Античная мысль.

Космологические представления, созданные античными мыслителями продолжили традицию представления мира в виде двух начал. Согласно Анаксимену и Гераклиту процессы формотворчества протекают в природе через разрежение и сгущение материальной субстанции - воздуха и огня. Самоизменяющийся и самоорганизуюшийся Сфэрос Эмпедокла представляет собой взаимодействие двух "энергетических"начал или сил, - Любви (дружбы, блага) и Вражды (ненависти, зла) и создает гигантский колебательный процесс, приводя Сфэрос в движение. Воцаряется, берет верх Любовь и однородное соединяется с однородным - Вражда отступает; с возобладанием же Вражды нарастает раздор, разъединение сущего и отступает Любовь. У Парменида бытие, под которым понимается все сущее берется в единстве с небытием или не сущим (то, что никак не определено и не оформлено). Началами же всех вещей у него фигурирует свет и тьма (Огонь и Ночь). Эти начала уравновешены, сомкнуты в гармонии, наличие которой есть проявление того, что существуют вещи, полные движения, переменчивости жизни и одновременно неподвижности, спокойствие вечности и смерти. У Платона космос, выстроенный демиургом, включает в себя ему неподвластные начала, - соединение однородного (тождественность) и разнородного (иного), спонтанного и планомерного, созидающего и разрушающего (Сороко, 1984). Общую ткань мира, служащую основой для всего возникающего, сущность которой является процесс, сохраняющий связность, Платон обозначает термином "Восприемница и Кормилица всего возникающего". "Платон говорит о нем, как о темном и трудном для понимания понятии (Платон, Тимэй). Уайтхед (Уайтхед, 1990) отмечает по этому поводу, что "пространство и время современной математической физики, понятое в абстракции от частных математических формул, почти в точности совпадает с "Восприемницей и Кормилицей" Платона."

В принятой у пифагорейцев символике каждая из десяти пар состояний (предел-беспредельное, четное-нечетное, единое-множество, правое-левое, мужское-женское, покой-движение, прямое-кривое, свет-тьма, хорошее-дурное, квадратное-продолговатое) фиксирует какую-то одну определенную сторону противостояния жизни и смерти, причем один полюс всегда в чем-то преобладает над другим (жизнь над смертью). Отметим, вслед за (Сороко, 1984) одно из достижений пифагорейцев - выделение четырех базисных элементов или четверицы (тетрактиды). Такими элементами являются точка, отрезок, треугольник, тетраэдр. В современной топологической терминологии они носят название симплексов, посредством которых выражают "мерность" пространства: нуль-мерное, одномерное, характеризующееся длиной; двумерное - "плоскостностью"; трехмерное - объемностью. Совокупность "точечных единиц" (1,2,3,4), используемых для построения всех названных базисных элементов, в сумме дает десять. Это число называлось пифагорейцами четверицей. Отметим асимметрию базисных элементов: один из них - точка, не существует в реальном мире, и в отличие от остальных является абстракцией. Цитируя Б.Беллюстина (Беллюстин,1923) Сороко пишет, что единица, по Пифагору, обозначала дух, из которого проистекает весь видимый мир. Из единицы происходит двойка, символ материального атома. Принимая в себя единицу, двойка или материальный атом, становится тройкой или подвижной частицей. Это символ живого мира. Живой мир плюс единица, следовательно четверка, образует целое, т.е. видимое и невидимое. Так как 10=1+2+3+4, то оно выражает собой "Все". Заметим, что в приведенной трактовке базисные элементы попарно имеют общую природу, а именно: единица и тройка обозначают подвижное живое , текучее, имеют "потоковую природу, а двойка и четверка нечто более застывшее, неподвижное, или имеют пространственную природу. Это принципиальное замечание, которое как мы увидим в дальнейшем, вообще всегда проявляется при более глубоком рассмотрении двойственности, как явления, имеющее более сложную, четырехэлементную структуру, вместо обычной, двусторонней, используемой при рассмотрении движения противоположностей. Четырехэлементный базис ("четыреяковость") использовал также Аристотель в его учении о четырех причинах противопоставления, четырех смыслах отношения предшествования, четырех разновидностях умозаключения, четырех видах качества, четырех значениях сущности и др. (Аристотель. Метафизика). Среди названных Аристотелем основных категорий четыре составляют самозамкнутый, внутренне полный тезис: количество, качество, отношение, сущность (Аристотель. Категории). Здесь также можно выделить пары: количество - отношение, качество - сущность, характеризуемые определенным единством их природы. Сороко приводит фрагмент, приписываемый видному пифагорейцу Филолаю - "Гармония вообще возникает из противоположностей. Ибо гармония есть соединение разнообразной смеси и согласие разногласного". Здесь внимательный взгляд также увидит парные соединения внутри противоположностей: соединение и согласие, смесь наряду с разногласием.

4. Двойственность. Диалектика Гегеля.

От древних мифов и античных ученых сразу перейдем к одному из великих мыслителей - Гегелю. Конечно, его не менее великие предшественники, такие как Декарт, Спиноза, Фихте, Шеллинг, Кант и др. тоже могли бы многое рассказать о двойственности, но это уже требует специального исследования. Нашей же целью было показать устойчивость двойственного мировоззрения, которое упорно пробивало себе дорогу, занимая умы лучших ученых всех времен и народов. В частности, именно Кант обнаружил парность категорий в синтетических суждениях. Его работы привели к ясному осознанию антиномий, которые порождаются именно этими категориальными парами. И со времен Канта принято говорить не о категориях, а о категориальных парах, т.е. материальное-идеальное, причина-следствие, форма-содержание, сущность-явление. В этом смысле мы даже не можем назвать одним словом это новообразование, которое состоит из двух взаимосвязанных, двойственных по отношению друг к другу категорий. Впрочем, попадаются и современные учебники, где один раздел посвящается категории явления, а другой - категории сущности.

Гегель - это один из тех гигантов мысли, которые до сих пор вызывают восхищение мощью "чистого" одиночного человеческого разума. Начав с простого (кстати, известного до него) утверждения, что "чистое бытие есть ничто" он выстроил целую "Науку логики" (Гегель,1998), как всеобъемлющий метод познания, который затем с немецкой последовательностью и педантичностью применил к построению философских теорий мышления ("Феноменология духа"), природы, истории.

Рассел (Рассел, 1999) считал теорию Гегеля заблуждением. Действительно, великолепный замысел обернулся благодушной констатацией: "Все действительное разумно, все разумное действительно" и зафиксировал, как высшее воплощение абсолютной идеи - в природе - ограниченное знание начала XIX века, в истории - оправдание насилия, в праве - господство государства над личностью. Поистине, "гора родила мышь". Почему так произошло и действительно ли философия Гегеля является ошибочной, только потому, что она привела его к указанным выводам. На наш взгляд, Гегель на самом деле заблуждался, но это заблуждение тоже было великим, - об этот камень преткновения до сих пор спотыкаются философы. Это проблема становления (или в гегелевской терминологии снятие противоречия между тезисом и антитезисом), которая до сих пор остается в центре внимания всех философских школ. Поскольку снятие (синтез) воплощается по Гегелю в абсолюте (абсолютном духе, абсолютной идее), который затем материализуется в человеческом духе, природе, истории и т.д., то в переходе от надчеловеческого к человеческому могут извлекаться произвольные трактовки, то есть синтез в мышлении ( впрочем, как и в природе) неоднозначен. Из одного и того же закона отрицания отрицания Гегель, например, выводил незыблемость и мудрость устройства прусского государства, а его горячий последователь Маркс-неизбежность революционного разрушения любого государства. Но Гегель велик, непререкаем и пока никем не опровергнут как раз там, где это важно для целей нашего исследования. Двойственные категориальные пары и образуемые ими "четверные петли" отношений пронизывают все разделы "Науки логики". Логическое единство теории, опирающееся на двойственность-наличие и взаимодействие двух неразрывно связанных понятий, отражает, на наш взгляд, органическое единство всего сущего.

Не углубляясь далее в дебри философии Гегеля, остановимся лишь на одном следствии, взятом из "Науки логики", которое важно для иллюстрации нашего предмета. Предвзятый знаток мог бы придраться к случайности выбора этого примера для иллюстрации двойственности. Ответ будет звучать по-современному: теория диалектики Гегеля самоподобна (фрактальна); из каждого раздела "Логики" можно извлечь одно и то же понимание двойственности и ее структуры. Рассмотрим соотношения "одно и многое". Гегель пишет (Гегель, 1998, ) - "одно оказывается совершенно несовместимым с самим собой, отталкивает себя от самого себя, и то, чем оно себя полагает, есть многое. Далее приведем наш перевод по подлинной работе Гегеля (Gegel, 1975). "Отталкивание, рассмотренное в нем самом выступает, как отрицательное отношение (Verhalten) многих одних относительно друг друга (gegeneinander), следовательно, их связь (Beziehung) соотносит их друг с другом. (aufeinander) и так как те, с которыми соотносится одно в своем отталкивании суть одни, то оно соотносится в них с самим собой".

Чтобы глубже уяснить смысл приведенного Гегелем положения, напомним, что в немецком языке Verhalten и Beziehung хотя и переводятся на русский язык как синонимы, которые означают "отношение, связь, поведение", на самом деле в оригинальном тексте имеют разный смысл. Если Verhalten-отношение, то это отношение "удержания, схватывания" откуда-то изнутри (на это указывает глагольное окончание halten-хватать, удерживать), обусловленное противоположением одного к многим как внешних друг к другу ( на это внешнее, как бы отталкивающее одно от многих указывает приставка gegen в слове gegeneinander). С другой стороны, Beziehung-это тоже связь, тоже отношение, но отношение вытягивания "вовне" (глагол zienen - тянуть, вытягивать), но имеющий природу внутреннего, как вытекающего из противополагания одного из многих (приставка auf в слове aufeinander). Таким образом, мы вновь имеем наличие в двойственном комплексе "одно-многое" четверки отношений, объединенных в пары Beziehung-Verhalten, и aufeinander- gegeneinander. Этой структурой обладают все знаменитые гегелевские формулы, например " основание есть внутри себя сущая сущность. Сущность есть существенным образом основание"; "сущность является, явление существенно". Это походило бы на игру слов, если бы на этом не была построена вся логика Гегеля. Что стоит за этим? Являются ли эти гегелевские "петли" умозрительными построениями или за ними стоит какое-то фундаментальное свойство природы и если да, то какое? Мы отвечаем на это утвердительно и считаем, что двойственная структура гегелевских утверждений - это попытка, так сказать, в нулевом приближении "ухватить" в словесном выражении беспрерывно меняющийся, развивающийся мир, который в каждый миг есть то, что он есть и в то же время не является тем, что он есть. А то, чем он уже не является обратно влияет на то, что есть в следующий момент времени и т.д. и этот переход от небытия к бытию - есть то, что отражается в категориальных парах Гегеля. К сожалению, эти тонкости философского смысла высказываний Гегеля полностью утрачены (как впрочем в других местах оригинального текста "Логики") при переводе на русский язык и эти ущербные места воспроизводятся вновь и вновь при очередных переизданиях.

5. Двойственность.Свидетельства ученых XX века.

Наш обзор философского понимания двойственности был бы неполон без упоминания хотя бы вкратце об идеях ряда философов XX века. Сразу оговоримся, что их выбор обусловлен ограниченностью целей данного обзора, призванного дать лишь общий абрис проблемы, и личными пристрастиями автора. Уайтхед - крупный математик и оригинальный философ (Уайтхед, 1990) сосредоточил свое внимание на динамическом описании реальности как процесса. В результате оказывается возможным избежать понятия "субстанция-качество". Это морфологическое описание заменяется описанием динамического процесса. "Каждое действительное явление проявляет себя как процесс; - оно есть становление". Уайтхед выделяет два вида становления: сращение и переход .

Первый вид становления (сращение) внутренне присуще процессу конституирования отдельно существующего. Второй вид становления (переход)-это становление, благодаря которому прекращение процесса в случае формирования отдельно существующего конституирует это существующее как изначальный элемент конституирования других отдельно существующих, которые выявляются при повторении процесса. Сращение направлено к своей конечной причине, представляющей его субъективную цель; переход же является механизмом действующей причины, которое есть бессмертное прошлое. У Богданова (Богданов, 1990) сохранение системы "есть результат подвижного равновесия системы с ее средой, т.е. образуется двумя потоками активности - ассимиляцией, поглощением активности извне, и дезассимиляцией, разусвоением активностей, их потерею, переходом во внешнюю среду; это означает два ряда непрерывных и параллельных процесса прогрессивного подбора: положительного и отрицательного. В каком направлении они регулируют развитие? Очевидно, в сторону наиболее устойчивых соотношений, ибо менее устойчивые отрицательным подбором должны постепенно отметаться ( в постепенно отметающиеся могут возникать "точки роста" для более устойчивых образований -В.П.), а более устойчивые - положительно закрепляться. Теперь можно видеть, что положительный подбор ведет к первому типу становления, который продолжает разворачивать цепь все новых и новых сущностей - цепь живого многое из которого тут же погибает, в иных случаях лишь обозначая возможность своего рождения. Отрицательный подбор связан со становлением второго типа - переходом и закрепляет рожденное сущее в системе постоянно воспроизводящегося мира и в этом смысле действительно является переходом постоянно рождающегося и умирающего живого к бессмертному неживому, формирующему прошлое.

По поводу существования двух видов становления Уайтхед делает проницательные замечания, - "имплицитное понимание двух видов становления было неосознанно присуще Юму. Кант едва не сделал его эксплицитным. Это понимание было утеряно в эволюционном монизме Гегеля и гегельянских школ".

Бом (Bohm, 1987) утверждая, что "эксплицитный порядок может рассматриваться как проявление развернутого (unfolding) более глубокого имплицитного порядка", приводит пример: водоворот в реке есть выражение полного течения реки и его структура постоянно поддерживается динамикой реки как целого. Можно сказать, что водоворот является динамическим инвариантом реки. "Реальность, - считает Бом, - проявляет себя через двойственное движение, в том смысле, что целое свернуто (enfolded) внутри индивидуальности и внутри каждой области пространства природа этой реальности может быть выявлена двояким (both) образом: вытягиванием наружу в эксплицитной форме (которое питает следующий имплицитный порядок) или движением внутрь к самому имплицитному порядку. В эмплицитном порядке тела являются внешними по отношению друг к другу и взаимодействуют через локальные силы. В противоположность этому в имплицитном порядке структуры охватывают (enfold) друг друга таким образом, что одна структура может быть внешней и внутренней по отношению к другой". Обратим внимание, что Бом при описании двойственности также оперирует "потоковой" моделью (пример водоворота в реке), описывая движение двойственной реальности в парных терминах explicit- unfolded, implicit-enfolded.

6. Двойственность.Примеры из специальных наук.

Математика. Простейшим примером проявления двойственности в математике является хорошо известное из школьного курса (Киселев, 1958) существования прямой и обратной теорем. Теоремой, обратной данной, называется такая теорема, условием которой служит заключение данной теоремы, а заключением - условие данной теоремы. Легко заметить, что если исходить из второй теоремы, названной нами обратной и считать ее прямой теоремой, то теорема названная прямой, окажется обратной. Поэтому часто говорят не о прямой и обратной теориях, а о двух взаимно обратных теоремах (Градштейн, 1973). Взаимно обратные или двойственные друг другу теоремы, истинность которых доказана, играют очень большую роль в математических исследованиях. Для изучения каких-либо объектов часто очень важно знать не только свойства данного объекта, но и то, какие из этих свойств можно принять за основные свойства, вполне определяющие данный объект. Эти свойства объектов (геометрических фигур, множеств) выделяются посредством доказательства обратных теорем. Таким образом, наличие двойственности позволяет выделить некую сущность объекта (основное свойство, инвариант)-факт, наиболее важный для понимания ценности двойственных утверждений.

В проективной геометрии двойственными являются точка и проходящая через нее прямая; в этом случае говорят о точке инцидентной прямой и о прямой инцидентной точке (Глаголев, 1963). Прямые, плоскости, объемы и так далее (собственные элементы пространства) в проективной геометрии замкнуты на бесконечности так называемыми несобственными элементами - соответственно бесконечно удаленной точкой, бесконечно удаленной прямой, бесконечно удаленной плоскостью и т.д. В основе проективной геометрии лежит полное равноправие собственных и несобственных элементов. Двойственной отрезку прямой является та часть прямой, которая дополняет отрезок до полной проективной прямой, замкнутой на бесконечности. Аналогично, ограниченной окружностью частью плоскости двойственна вся внешняя часть плоскости, дополняющая круг до полной проективной плоскости. Принцип двойственности в проективной геометрии утверждает, что если верно какое-либо предложение, касающееся точек, прямых плоскостей и отношений инцидентности между ними, то верно и так называемое двойственное предложение, получаемое из данного, если поменять слова "прямая" и "точка" ( для проективного пространства слова "плоскость" и "точка").

Примером двойственности является задача линейного программирования (Карманов,1986). Прямая задача заключается в нахождении максимума целевой функции внутри выпуклого многогранника, расположенного в n-мерном пространстве. Многогранник задается линейной формой с "n"- ограничениями, наложенными на m-мерный вектор-аргумент целевой функции. Обратная или двойственная задача-нахождение минимума обратного функционала снаружи на поверхности многогранника, в пространстве m-мерной размерности. При этом компоненты "прямого" вектора преобразуется по соответствующим правилам обращение матриц в коэффициенты-ограничения для обратной задачи.

В теории категорий (Букур, 1972, Паленко 1974) категорию К* двойственную к категории К определяют как категорию с теми же, что и у К объектами, но с морфизмами (отображениями) действующими в обратную сторону. Примерами категорий являются категории множеств, топологических пространств, групп и др. Каждый объект А из К может быть помечен знаком "*" и объявлен объектом категории К* ; каждый морфизм f : А®В также помечается знаком " * " и объявляется морфизмом f * : В*®А*. Категория (К*)* отождествляется с категорией К. С каждым высказыванием, сформулированным на языке теории категорий связывается двойственное высказывание, которое получается интерпретацией исходного высказывания в двойственной категории. Другой способ получения дуального высказывания состоит в сохранении логической структуры исходного высказывания и обращения порядка встречающихся в нем "множителей" (обращение стрелок). Принцип двойственности для теории категорий утверждает, что некоторое высказывание истинно тогда и только тогда, когда в этой теории истинно двойственное высказывание. Принцип двойственности позволяет выделить формальные связи между понятиями и результатами, которые в конкретных категориях, кажутся не зависящими друг от друга. В частности, с помощью теории категорий была найдена двойственная связь между наблюдаемостью и достижимостью системы. Наблюдаемость понимается в смысле возможности определить состояние системы по выходу. Достижимость в определении множества достижимых состояний. Система представляется как пара двойственных систем, таких, что достижимость одной двойственна ( в смысле категории) наблюдаемости другой.

Физика. Интересный пример двойственности представляет рассмотрение закона тяготения. Ньютоновская формулировка закона говорит, что сила тяготения зависит от масс тел, находящихся на конечном расстоянии. Она обладает свойством нелокальности или дальнодействия (Фейнман, 1968). Сила, действующая на предмет, зависит от того, насколько удален от него другой предмет по закону обратного квадрата расстояния. С другой стороны существует иная трактовка закона тяготения, основанная на понятии поля. Если теория дальнодействия оперирует понятием силы, которая является вектором, то в полевом описании каждой точке пространства приписывается число-потенциал, который является уже не векторной, а скалярной величиной. При переходе от точки к точке это число меняется, а сила, действующая на тело, действует в направлении быстрейшего изменения потенциала. В отличие от дальнодействия потенциал в центре сколь угодно малой сферы определяется тем, каков потенциал по соседству с интересующей нас точкой и какова масса, заключенная внутри сферы. Эта формулировка локальна во времени и в пространстве, потому что она говорит о соседних точках. Она является двойственной формой описания обычной ньютоновской формулировки, которая во времени непрерывна, а в пространстве дискретна.

В электродинамике примером двойственных соотношений являются фундаментальные уравнения Максвелла, описывающие распространение электромагнитных волн в пространстве. В случае отсутствия токов и зарядов уравнения приобретают наиболее симметричную форму: одна пара уравнений получается из другой простой заменой вектора напряженности электрического поля Е на вектор магнитной индукции B. Наличие токов и зарядов усложняет картину, но двойственность по-прежнему проявляется, приобретая теперь уже иной облик, связанный с различной симметрией векторов Е и В. Отсутствие магнитных зарядов приводит к тому, что вектор В в отличие от вектора Е всегда имеет вихревую природу, будучи порожденным благодаря изменению токов и электрической напряженности. Геометрически величина вектора такого типа определяется элементом плоскости, в отличие от вектора напряженности электрического поля, которому можно сопоставить направленный отрезок. В этом случае говорят соответственно о контрвариантном и ковариантном векторах, законы преобразования которых при изменении координат взаимно обратны. Таким образом, физическая взаимообусловленность векторов Е и В имеет под собой глубокий двойственный геометрический смысл, аналогичный инцидентности прямой и плоскости.

В физике широко используются понятия интенсивных и экстенсивных величин. Первые отвечают на вопрос "как сильно?" ; последние - "как много?". Первые имеют характер силы, вторые являются количествами действия первых. Говорят также соответственно об обобщенных силах и обобщенных скоростях или потоках.

В случае электрических явлений, например, напряжение является своеобразным действием, т.е. интенсивной величиной (обобщенной силой), тогда как сила тока есть количество, т.е. экстенсивная величина (поток заряда). В 1931 году Ларс Онзагер обнаружил, что в равновесных системах между обобщенными силами и потоками существуют замечательные соотношения взаимности (Пригожин, 1986) . Для слабо неравновесных электрических явлений справедливо следующее: если сила "один" (например, градиент потенциала электрического поля( воздействует на поток "два" (поток заряда), то сила "два" (градиент распределения зарядов) воздействует на поток "один" (поток электрического поля). Причем это происходит таким образом, что эти воздействия направлены в противоположную сторону и стремятся вернуть систему к равновесию ( в данном примере это проявление самоиндукции). Нетрудно видеть, что соотношение взаимности есть не что иное как проявление двойственности, причем на более высоком структурном уровне. Что здесь понимается под усложнением структуры отношений обобщенных сил и потоков? Во-первых удвоение пары отношений "сила-скорость" и появление четверки понятий (две обобщенных силы и две обобщенных скорости): во-вторых их взаимопереплетение ( причина "один" становится следствием "два" и наоборот) и, наконец, динамический характер переноса энергии, вещества, информации, указывающий на изменение, развитие системы, стремление ее к определенному состоянию.

В термодинамике первое начало связывает полный дифференциал dU (функцию состояние системы U) с двумя неполными дифференциалами dА и dQ, где А и Q соответственно работа и теплота. Следовательно, работа и теплота, является по отдельности "неполными" характеристиками системы, причем как в физическом смысле (описывая лишь один из двух способов энергетического воздействия на систему), так и в математическом (будучи неполными дифференциалами, то есть не являясь функцией состояния системы) дополняют друг друга "до полной" характеристики (внутренней энергии) и тем самым представляют собой две двойственные структуры в одном "энергетическом" теле, связанные первым началом термодинамики. Для равновесных процессов dА= Pdv и dQ=TdS, где P-давление, V-объем, Т-температура, S-энтропия . Экстенсивные параметры V и S называют обобщенными координатами, а интенсивные параметры P и Т -обобщенными силами, причем, "сила" P сопряжена с координатой V, а сила Т с координатой S. Между этими парами параметров (P,V) и (Т, S) существует взаимно однозначное соответствие; так называемый якобиан перехода (Румер, 1977) от одной пары к другой равен единице, что делает равноправными координатными плоскости (P, V) и (Т, S). Отметим, что ассиметрию в четверке P, V, T, S; если первые три параметра являются реально измеряемыми величинами, то энтропию измерить невозможно. Указанная четверка является параметрами двойственных понятий более высокого уровня - четырех термодинамических потенциалов: внутренней энергии U(V, S), свободной энергии F(V,T), энтальпии H( P,S) и потенциала Гиббса G(P,T). Каждый такой потенциал является функцией двух параметров, один из которых принадлежит паре (P,V), а другой (T,S). Можно показать, что V, F, H, G связаны между собой отношениями двойственности.

При всем многообразии проявлений двойственности самым поразительным и в то же время фундаментальным свойством материи является дуализм вещества и волн. Известно, что свет проявляет себя при одних условиях как ньютоновская частица, а при других как волна. То же самое справедливо для электрона, протона и любой материальной системы. В зависимости от вопроса, который мы задаем микрочастице, она поворачивается к нам то своей волновой, то корпускулярной природой. То обстоятельство, что на эксперименте никогда не возникает логического противоречия между обоими представлениями обеспечивается соотношением неопределенности Гайзенберга, утверждающего, что невозможно одновременно локализовать положение частицы вместе с точным знанием ее импульса. Мерой определенности одновременного обнаружения частицы и измерения ее импульса является планковский квант действия (AxA~h, где h - постоянная Планка) (Фейнман, 1967).

Химия. Химические реакции стремятся протекать в направлении уменьшения свободной энергии. Напомним, что свободная энергия-это понятие, указывающее на максимальную величину работы, которую можно получить в результате той или иной химической реакции, при условии теплового контакта с окружающим внешним миром. Можно провести механическую аналогию между поведением системы из двух грузов и химической реакцией (Эткинс, 1987). Так тяжелый груз, падая ( двигаясь в "естественном" направлении) может поднимать более легкий груз (если грузы, скажем, соединены между собой нитью, перекинутой через блок), вызывая его движение в "противоестественной направлении ( против сил тяжести). Реакция подобна грузу, но "падающему" в направлении снижения не потенциальной, а свободной энергии. Химическая реакция, более глубоко опускающаяся по шкале свободной энергии может вызвать протекание связанной с ней реакции в противоположном направлении (такие реакции в биохимии называют сопряженными ( а в нашей терминологии - двойственными - В.П.).

Развивая механическую аналогию, Эткинс предложил наглядную картину живой системы. Живые организмы и клетки можно уподобить чрезвычайно сложной системе зацепляющихся друг за друга шестеренок (кстати, шестеренчатые передачи в механике - это также пример двойственных систем, служащих для передачи мощности - В.П.). Если в какой-то части организма "тяжелый груз" падает по шкале свободной энергии, то в другой ее части "легкий груз" за этот счет может подняться вверх по этой шкале, но на меньшую величину. Механизм такой биохимической "зубчатой передачи", разумеется весьма деликатен и сложен. Хотя организм в целом, движется по пути деградации, т.е. по пути понижения свободной энергии, эти процессы столь сложны и взаимосвязаны, что попутно рождаются все тончайшие явления, соответствующие жизни и сознанию. Именно поэтому нам необходимо питаться: мы усваиваем вещества, находящиеся достаточно высоко по шкале свободной энергии, а затем в организме они начинают распадаться, вызывая вращение внутренних "шестеренок" организма.

Биология. Фундаментальным примером двойственности является кодирование генетической информации. Наследственную информацию, содержащуюся в ДНК и РНК, кодируют вообще-то два класса азотистых оснований-пирины и пирамидины (Инге-Вечтомов,1983). Они образуются из пяти видов нуклеотидов: тимин, аденин, гуанин, цитозин, урацил. Четыре первых кодируют ДНК, четыре последних РНК. Два пуриновых основания-аденин и гуанин составляют инвариантную часть обоих соединений, ДНК и РНК. Именно наличие этих двух общих оснований, входящих по одному в качестве "особых" элементов в кодирующую четверку (остальные три являются пиримидинами) позволяет осуществлять процесс репликации. Двойная спираль стабилизируется с помощью водородных связей между пуринами одной цепи ДНК и пиримидинами другой. В результате образования строго определенных пар аденин-тимин, гуанин-цитозин, последовательность оснований одной цепи однозначно определяет ее последовательность в другой - иными словами цепи двойной спирали ДНК комплиментарны (Франк-Каменецкий, 1988).

Открытие двойственной структуры ДНК сыграло в развитии биологии такую же роль как и физика открытие атомного ядра, привело к появлению молекулярной биологии, а в последние годы генной инженерии.

Двуликий Янус биологии - структура и функция. По мнению Гамалея (Гамалей,1999) развитие структур детерминировано генетически, реализация функций экологически. Генетически наследуемые структуры выполняют в эволюционном развитии стабилизирующую роль, закрепляя пройденный путь, а экологически зависимые функции -раскачивающую, обеспечивающую поиск направления движения сегодня. Путем участия обоих регуляторных механизмов достигается совмещение направленной (прогрессивной) и адаптивной составляющих эволюции в точке перехода прошлого в будущее. Влияние структуры на функционирование понятно; ей задан диапазон подвижности, амплитуда функциональных колебаний; влияние функциональных колебаний на изменение структуры менее видно, ее механизм - постепенное накопление ничтожно малых сдвигов. Эти изменения хотя и очень малы, но необратимо накапливаются. Биологическое время изменяется структурами как вехами пройденного пути. По функциональным признакам воссоздания структуры практически невозможно.

Вертикальная детерминированность структурного развития и горизонтальная - функционального дают основания поставить задачу поиска модели, отражающей четырехмерные отношение текущей экологии и эволюции. С ее помощью можно, видимо, описать перекрест времени и пространства в биологической системе координат. Структура отражает пройденный путь, функциональный трепет- выбор направления движения, поиск следующего шага. Экологическая подвижность функций в диапазоне заданном структурным исполином прошлого, дает некоторое основание предположить вибрационную модель функционального поиска продолжения эволюционного пути в условиях определенной экологии.

Диалектическая логика. Гегель показал, что все подлинные понятия, которыми пользуется разум, обязательно содержат внутри себя категориальные пары. Совершив этот шаг, он получил возможность сделать то, что не мог сделать ни один логик по профессии до него: он дал первую классификацию логических форм, указывая на их отличие от грамматических форм.

Известно, что суждение представляется в виде "субъекта" и "предиката", соединенных связкой "есть". Если субъект есть нечто единичное, а предикат нечто всеобщее, то мы имеем дело с логической формой сужения. Так, грамматические предложения типа: "Иван есть человек", "Жучка есть собака" представляют собой суждения. Логической основой для выделения логической формы суждения является простой факт, что связка "есть" связывает "категориальную пару" или "диаду".

Наивная уверенность старой формальной логики состояла в том, что суждения делятся на два класса: на истинные и на ложные. Здравый смысл будет возражать, если кто-то будет утверждать, что "единичное есть всеобщее" или что "причина есть следствие". Какое же из двух суждений антиномии следует считать истинным? Ответ будет краток: никакое. Гегель показал, что форма суждения не является той логической формой, в которой вообще выражается истина. Логической формой истины является по Гегелю "умозаключение". В ее состав входят логические формы суждения, а логической форме суждения (диаде) предшествует и входит в нее логическая форма понятия.

Логическая форма понятия сама состоит из двух различных логических форм: пары единичное - особенное, единичное - всеобщее, особенное - всеобщее образуют "диады", а их целостность, своеобразная независимость от логической формы диады требует своего названия - "триады". Эти две логические формы, еще не различавшиеся Гегелем на правах логических форм (Кузнецов П.Г., 1988) лежат в основании математики. Их выделение стало возможным тогда, когда Н. Бурбаки в анализе основных математических структур сумели выделить две качественно различные математические структуры. Их намечавшиеся названия примерно соответствуют "закону композиции" и "отношению порядка". Их философское содержание, которое лежит за рамками математики и принадлежат к логическим формам, обозначается логической формой диады и логической формой триады.

Математической формой записи логической формы "диады" являются формулы, в которых соединяются знаком равенства два выражения, отличающиеся друг от друга по написанию (А=В) и в левой , и в правой части этой формулы могут быть понятия, отнесенные к одной из двойственных пар, входящих в триаду и задающих "отношение порядка", "направление", "ориентацию". Внематематической формой этого "следования" и является логическая форма "триады". Поэтому простейшая логическая форма умозаключения должна учитывать это обстоятельство и тогда вместо одной формы записи (А=В) мы получим четыре:

А = не В; не А = В; В = не В; А = не А.

Вместе с первоначальной записью А = В теперь имеем минимум пять формул. Мы сумеем лучше уяснить всю глубину этих кажущихся удивительными для здравого смысла выражения, если расположим их в следующем виде:

Это опять та же структура, с которой мы уже встречались при рассмотрении соотношения одного и многих через Гегелевское понятие "отталкивания". Откуда же она взялась? Мы добавили и добавили вполне обоснованно, исходя из логики движения к первоначальной записи частицу "не" - , так как в изменяющемся мире А есть В и А не есть В.

Лингвистика. Простым и наглядным примером двойственности является письменный язык. Когда Вы читаете эти строки мозг считывает информацию, содержащуюся в знаках - буквах, расположенных по определенным правилам в двумерном пространстве, - на листе бумаги. Отношение порядка задается направлением считывания букв - справа налево (хотя существуют языки, где направление противоположно, например, - иврит) или направлено по вертикали - пример, - иероглифы). Кроме того, дополнительные отношения порядка определяются морфологией-правилами образования слов из букв. Таким образом, образуется каркас ("скелетная форма"), и теперь дело за композиционным отношением - грамматикой - сводом правил, в соответствии с которыми из отдельных слов и знаков препинания образуются предложения, несущие информацию. Полученная система обладает большой гибкостью и способностью к приспособлению; ведь после любого написанного текста у нас есть многозначный выбор формулировок, с которыми его можно продолжить. Но эти возможности не безграничны, существует еще одна глобальная двойственная система, которая формируется всем окружением каждой фразы - это контекст. И без нарушения внутренней логики содержания невозможно перейти к изложению чего-либо, иначе, речь будет в каждой части морфологически и грамматически неправильна, потеряет связность. Потеряв это свойство речь становится бессвязной, не характерной для здорового человека. Итак, с видимым текстом на этой странице (материальными знаками, исполненными в краске, написанными на плоскости бумаги) связан невидимый, двойственный текст (контекст), который невозможно увидеть физически. Этот "двойственный" текст заключен в тех же материальных структурах, что и прямой текст, но прочитать его можно только "погрузив" прямой текст в мыслительный аппарат человека. Этот аппарат должен быть достаточно развит, чтобы принять эту конструкцию, - например ребенок, который учится читать, складывать слова из букв, в течении определенного времени, пока мозг не натренируется, не способен воспринимать контекст.

7. Двойственность. Теоретические модели².

Тектологическая модель.

"Комплекс" - писал Богданов (Богданов, 1989) заключен в своей среде одновременно и как отливочный материал и как формовочная модель, определяясь этой средой в первом смысле и частично определялся "во втором". Образ формовочной модели и отливочного материала является прекрасной иллюстрацией к статической модели двойственности. Комплекс Богданова не является простой коллекцией элементов и их соотношений, он представляет собой процесс или непрерывный поток независимых генерирующих элементов - процессов заключенных в круги построения и деградации. (Zeleny, 1999). Комплекс Богданова нельзя отделить от его окружения, так как он просто не существует или не взаимодействует вне этого окружения; он структурно связан с окружением и таким образом создает свое собственное окружение, вступая с ним в совместное развитие. Структурная связь с окружением исключает абсолютное отделение комплексов и устанавливает их общую систематическую конвергенцию или дивергенцию (сходимость или расходимость), что приводит к все более возрастающей комплиментарности или дополнительности элементов и их соотношению.

Богданов ввел понятие регулятора (современная обратная связь), как устройства, благодаря которому процессы сохраняются на определенном уровне (например, маховик). Он пошел значительно дальше и ввел понятие бирегулятора, то есть систему взаиморегулирующих одна другую без внешнего регулятора; они взаиморегулируются. Это два аспекта единой системы равновесия. Бирегулятор это не простая обратная связь, а двусторонняя динамическая система. Термостат не только регулирует температуру, но и температура регулирует термостат, это осуществляется взаимно колебательным и неиерархическим способом. Любой комплекс должен ассимилировать (поглощать) и дезассимилировать (рассеивать) требуемое разнообразие окружения, с которым он структурно связан. Каждое изменение и сохранение за счет ассимиляции балансируется противоположными изменениями дезассимиляционных процессов. Таким образом устанавливается динамическое (или подвижное) равновесие. По мнению Богданова простые элементы комплекса связаны в узлы, цепи, причем линейные цепочки ингрессивно связаны в нелинейные и круговые цепи, постоянно и непрерывно строящиеся в цепочки более высокого порядка. Его связи: цепочки и сети (схемы) были началом предложенной им "математики сложности". Для понимания динамики комплекса требуется четкое разграничение между организацией и структурой системы. Организация относится к сети процессов генерирующих элементов (правила взаимодействия), а структура относится к определенной пространственно-временной модели. Основной моделью в исследованиях по устойчивости сложных систем является относительно твердый "скелет", погруженный в подвижную, изменяющуюся среду. Им приводятся различные примеры, когда системы, обладающие такой структурой являются наиболее способными к развитию и самоорганизации.

Информационно - энтропийная модель.

Эта модель (Сороко, 1984) исходит из того, что в структурно определенных системах информация вместе с энтропией представляет сохраняющуюся величину или:

энтропия (Н) + информация (I) = const

Информационная энтропия Н в количественном смысле совпадает с точностью до постоянного множителя с термодинамической энтропией S. То обстоятельство, то информация и энтропия перестановочны, исчислимы в одних единицах, позволяет образовать единую систему, на которой крайние точки - экстремальные значения количества информации и энтропии. Всякой структуре объекта, представляющего собой систему соответствует некоторая промежуточная точка этой шкалы - изображающая точка данной структуры. Если переписать вышеприведенное соотношение в виде (нормировка на единицу): H + I = 1 , то изображающая точка будет двигаться в интервале [0,1]. Ее движению в ту или другую сторону соответствуют: 1) процесс структурогенеза, типичный для самоорганизующихся систем, строящих свое поведение на основе саморегуляции, обратной связи; 2) процесс деградации, распада структур, типичный для всех изменений, совершающихся в сочетании со вторым началом термодинамики, то есть характеризующийся возрастанием энтропии. Изображающая точка структуры есть своеобразная граница между разнообразием и однообразием, множественностью и единством, необходимостью и случайностью, симметрией и асимметрией и т.д. (в зависимости от того, какое из структурообразующих отношений принято за основу). Сохранение соотношения "энтропия-информация" для конкретного объекта (это адекватно установленных определенных значений координат изображающей точки) может означать, что его структура достигла своего стационарного (устойчивого) состояния. Это случай "неустойчивого равновесия" (Бриллюэн, 1980), "или проточной устойчивости" (Bertalanffy, 1953).

Комбинаторно-волновая модель.

"Вероятностный подход - один из трех возможных в определении понятия количества информации: два других - алгоритмический и комбинаторный (Колмогоров, 1965). Случайность с ее логической независимостью событий - основой стохастических законов и необходимость с ее логикой, воплощенной в алгоритмах, в законах жесткой детерминации, - два противоположных, самостоятельных, начала отсчета." (Сороко,1984).

Комбинаторный подход в определении понятия "количество информации" сочетает в себе особенности вероятностного и алгоритмических подходов. Основной материал, на котором раскрывается его специфика. - алфавиты. Под алфавитом понимается любая базовая система знаков, каждый из которых есть самостоятельная единица, несущая минимальную смысловую нагрузку. Различные комбинации и сочетание этих знаков дают "слова", из которых образуются "предложения", аналогично тому, как это происходит в естественных человеческих языках. "Общие принципы формирования сложных систем из составляющих их элементв (молекул из атомов, организмов из клеток, биологических популяций из особий и т.д.) совпадают с теми признаками, по которым из букв алфавита складываются слова, из слов - фразы, а из фраз - сложные сообщения. Говоря кратко, действительность - это Текст. (Седов, 1978). Но мир в целом и в каждой своей структуре наряду с этим есть Волна (Налимов В., 1982) - структурный резонанс субстрата, из которого образованы все вещи, то есть своего рода. "интерференция" противоположности внутри единства. Двойственные стороны равноправны в своем целом, а, следовательно, любая из них заполняет собой все "пространство отношения" и интерферирует с другой, образуя "узлы" неподвижности субстрата. "Волнение" испытывает крайне абстрактная "материя" - субстрат систем, частотные (вероятностные) распределения их состава. Модель Мир - Текст, Мир - Волна кажется весьма трудным для понимания, но резонанс кооперативных явлений довольно часто встречается в природе (солитоны, явления сверхпроводимости и сверхтекучести, ячейки Бенара, химическая реакция Белоусова - Жаботинского и т.п.). Более наглядно сочетание комбинаторного и непрерывного подходов реализовано в следующей модели.

Тензорная модель.

Американский инженер - электротехник Габриэль Крон в своих исследованиях, посвященных теории обобщенных электрических машин и методу решения искомых задач по частям (диаконтика) (Крон, 1978) создавал и эффективно применял на практике электрические (в обобщенном виде - тополого-волновые) модели для решения технических, физических, статистических, экономических и любых других задач большой размерности. В своих уникальных моделях, (которые весьма трудны для восприятия, так как формируются из понятий как минимум трех областей знания: техники, математики, физики) ему удалось описать реальные задачи на двойственном языке, совмещающем преимущества топологического (структурного) и функционального (композиционного) подходов.

Крон постоянно использует двойственные понятия именно как метод и убедительно показывает эффективность такого подхода. На "мертвую" подлежащую сеть, отражающую отношение порядка Крон, накладывал "живую" электромагнитную структуру, связанную законом композиции. Это единство описания позволило Крону не только предложить универсальный метод решения сложных задач по частям, но и обнаружить замечательное свойство самоорганизации систем, образуемых "погружением" структурного "скелета" (понятия с его триадической структурой) в живую ткань изменяющейся среды, ограниченной проницаемой "оболочкой" (задаваемой законом композиции - "диадой"). Рассмотрим это более подробно. Аналогом понятия активность-сопротивление является импеданс, приписываемый простейшей одномерной сети - отрезку (одномерный симплекс или кратко 1 - сеть). Одномерные симплексы путем матричных преобразований могут объединяться в 2 - сети (аналог обычных электрических схем на плоскости), 2 - сети служат строительным материалом для объединения их в пространственные, 3 - сети и т.д., вплоть до многомерного обобщения (n - 1) - сети (где n - число линейных графов- импедансов). Понятно, что все сети одной размерности двойственны (изоморфны) друг другу, что выражается в существовании ортогональной квадратной матрицы преобразования, С; в случае перехода от сети одной размерности к другой матрица преобразования С становится прямоугольной. Именно такие топологические структуры Крон называл "мертвой", или подлежащей сетью.

Следующий шаг состоит в "оживлении сети", наложению на нее воздействий. В простейшем случае 2 - сетей накладываются токи и напряжение (I и и), где I и е - векторы, с компонентами I и е, приложенным к единичным импедансам. В результате в сети появляются отклики Е и i (также векторы той же природы), связанные с наложенными токами и напряжением "законом композиции" Ома

e + E = Z (i + I),

где Z - тензорная величина с компонентами, приписываемыми отдельным (диагональным элементам) и взаимным (все остальные члены) импедансам. В случае перехода от одной сети к другой (аналог развития) тензор (и соответственно векторы Е, i, I, e) преобразуется с помощью матрицы С, по закону "порядка"

Z*= CZC_t^-1 и е* = C_t^-1e,

где Z* и e*- компоненты тензора и вектора в новой системе координат (в новой сети), C_t^-1 - обратная матрица к С. При дальнейшем обобщении модели двумерные сети могут заменяться многомерными, а вместо четверех параметров появляются все-более сложные характеристики электромагнитного поля (напряженность электрического и магнитного полей, плотность зарядов и т.д.). При этом с каждой из прямой p-сети связана двойственная ей (n - p) - сеть; например, в двумерном случае двойственной к узловой является контурная сеть, и наоборот.

Суть пионерского метода Крона состоит в том, что рассчитав простейшую электрическую машину он, с помощью тензорных преобразований смог получить результат для любой другой сколь угодно сложной электрической машины. Очень важно, что Крон установил универсальный закон: чтобы получить правильное преобразование от одной машины к другой необходимо рассматривать именно две сети - прямую и двойственную ей ортогональную сеть, так как только в этом случае сохраняется инвариант - мощность, рассеиваемая в сети.

И наконец диакоптика - это метод разрывания, использующий двойственный подход по отношению к задаче преобразования. Эта задача очень сложная: по функциональным признакам, возникающим в точках разрыва, необходимо восстановить структурно-функциональные особенности каждой из частей, а затем обратным преобразованием получить искомое решение. Последние годы жизни Крон (умер в 1968) много занимался так называемыми "полиэдральными" автоматами. В своих работах он показал (Крон, 1960), что многомерный полиэдр и двойственный ему ортогональный полиэдр, погруженные в электромагнитную плазму, образуют немеханическую осциллирующую структуру, в основе действия которой лежит сложное взаимодействие (нериманова динамика) обобщенных вращающихся электрических машин. Осциллирующий автомат, как показал Крон, способен к самоорганизации, самоподстройке под различные налагаемые параметры.

8. Двойственность. Нелинейность. Неутойчивость. Хаос. Фракталы.

В этом разделе мы ограничимся приведением примеров и комментариями к ним, почерпнутыми из работы (Николис,1990), делая, безусловно, оригинальный акцент на рассматриваемой проблеме двойственности.

Начнем с того, что в естественных науках, выделяются два вида систем: консервативные, динамика которых не зависит от направления времени (инвариантна относительно операции обращения времени, или замены в уравнениях t на -t) и диссипативные, демонстрирующие необратимость времени или зависимость их будущего состояния от прошлого, в том смысле, что прошлое в каждый момент времени вмонтировано в текущее состояние и определяет будущее. Строго говоря, консервативных систем в природе не существует, - речь может идти только о моделях, пригодных к использованию при вполне определенном условии, - когда удается пренебречь влиянием внешней среды или окружением или представить задачу в квазиконсервативном виде (например, классическая задача идеального маятника, которого не существует, может быть сведена в квазиконсервативной системе реального маятникового механизма в часах, получающих подпитку энергией извне). Квазиконсервативные системы широко применяются в технике, поскольку обладают свойством предсказуемости и многократного идентичного воспроизведения, так как они не зависят от времени. Значительно сложнее обстоит дело с диссипативными системами, характерными для природы, мира живого, мира человека. Свойство диссипативности предполагает наличие окружения, внешней среды с которой непрерывно происходит обмен энергией, информацией, материей, то есть в нашем контексте дисситпация и поток, активность - сопротивление - это одно и то же.

Самоорганизация вещества, приводящая к сложному поведению при всем множестве примеров (Николис,1990) сводится к трем основным типам, каждому из которых соответствует определенный вид двойственности. Это: 1) бистабильность и гистерезис (существование двух, взаимно поддерживающих друг друга ветвей: пример реакция Белоусова-Жаботинского, оптическая бистабильность в лазерах и др.); 2) колебания (периодические и непериодические (две фазы, переходящие одна в другую) и 3) пространственные фигуры (связанные с особым проявлением двойственности - фракталами). Разбирая возможность описания сложного, которое всегда связано с крупномасштабной когерентностью и согласованным поведением, необходимо отметить, что полная упорядоченность в виде полного отсутствия изменчивости представляет собой предельный случай когерентности, когда поведение объекта настолько примитивно, что едва ли можно говорить о сложном. С другой стороны, сильная изменчивость, представляемая случайным шумом и сопутствующее такой изменчивости отсутствие корреляций являются другой, столь же непредставительной формой организации. Сложность реальных систем должна находится где-то между этими пределами и, соответственно, описываться в моделях, учитывающих структурные и композиционные отношения. В дальнейшем мы покажем, что эти две стороны взаимно порождают и поддерживают друг друга.

В общем виде идею того, что на эволюцию системы влияет изменение некоторых характерных для данной задачи параметров, задаваемых внешней средой можно записать в виде:

dx_i/dt=F_i({X},Y)

где {X_i}- набор переменных состояния; Y- набор параметров, которые могут быть изменены внешним миром. Для стационарного состояния (даже неравновесного) F_i({X},Y)= O. В линейных системах (то есть, где X = kY) езультатом совместного действия двух факторов является их простые суперпозиции. Однако, в нелинейных системах небольшое увеличение внешнего воздействия может привести к очень сильным эффектам, несоизмеримым по амплитуде с исходным воздействием. Нелинейность всегда порождается двойственным процессом: например, в механике жидких сред скорость изменения той или иной характеристики начинает зависеть от переноса этой характеристики за счет течения среды, скорость которого является одной из переменных данной задачи. Особый интерес представляют нелинейности, связанные с регуляцией (вспомните бирегулятор). В этом случае некое вещество X может резко ускорить или замедлить собственное производство или производство другого компонента, в свою очередь замкнутого на первое вещество.

Как мы уже отмечали, диссипативные системы контактируют со сложным и даже непредсказуемым окружением. Это окружение непрерывно сообщает системе небольшие (реже значительные) количества вещества, импульса или энергии. С другой стороны в самой системе, каждая из ее частей также находится в окружении собственной среды и также может испытывать колебания внутреннего состояния - флюктуации. Этот вездесущий двойственный факт непрерывного изменения выражается математически в том, что мгновенное состояние X(t) cистемы не совпадает со стационарным состоянием Xs - оно представляет собой некоторое соседнее состояние:

(1) X(t)=X_s +x(t),

где x(t) - называется возмущением. Каким же образом система отвечает на такие отношения? Список всех возможных вариантов исчерпывается четырьмя случаями:

1. Состояние X(t) локально неустойчиво, но глобально устойчиво. Оно остается в некоторой окрестности стандартного состояния при всех временах, превышающих начальное время. Система колеблется возле стандартного состояния.
2. Состояние X(t) локально и глобально устойчиво. Диссипативная система устраняет возмущение и восстанавливает стандартное состояние. Состояние X_s называется аттрактором (асимптотическая устойчивость)
3. Состояние X(t) локально и глобально неустойчиво. Существует такое начальное возмущение, для которого амплитуда X(t) резко (обычно по экспоненциальному закону) растет и вся система "уходит" совершенно в другое состояние.
4. Состояние X(t) локально устойчиво, но глобально неустойчиво. Система остается в некоторой окрестности стандартного состояния X_s, если возмущение не превышает некоторого порового значения и удаляется от него в случае возмущений, превышающих пороговое.

Можно переписать уравнение (1) в виде x(t)=X(t)- X_s, и представить, что x(t)=f(g), где l - назовем управляющим параметром.

Теперь при малых l возможно лишь одно решение, соответствующее ситуации (2); эта область подобно равновесию характеризуется важным свойством асимтотической устойчивости - система способна гасить внешние возмущения и внутренние флюктуации.

При переходе через критические значения параметра l=l_c состояние становится неустойчивым, так как флюктуации или внешние возмущения уже не гасятся. Действуя подобно усилителю, система резко отклоняется от стандартного состояния и переходит к новому режиму. Оба этих режима сливаются при l=l_c и l>l_c . Это явление называется бифуркацией.

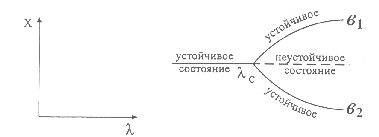
В решающий момент (в окрестности l=l_c) система должна совершить критический выбор. Решать будет лишь случай через динамику флюктуаций. Какая-то особенная флюктуация побеждает и система приняв ее за отправную точку превращается в своебразный исторический объект в том смысле, что его дальнейшая эволюция будет зависеть от этого критического выбора. Понятно, что сделанный системный выбор в пользу одной из ветвей (b₁ или b₂) может вновь привести к дальнейшему процессу, аналогично описанному и система продолжает свое развитие. Отметим, что, "победившее", скажем, состояние b₁ становится источником новых флюктуаций и внешних реакций. Можно отождествить флюктуации и внешние воздействия со структурными изменениями ( как в микро, так и в макрообластях), а поиск устойчивого состояния с стремлением к простой композиции, обладающей наименьшей энергией. Можно отметить сходство между этими представлениями и понятиями мутации и отбора в теории биологической эволюции. Флюктуации являются физическим аналогом мутации в то время как поиск устойчивости играет роль естественного отбора. Даже сама диаграмма бифуркации по своему устройству напоминает филогенетические деревья, широко используемые в биологии. Укажем также еще на одно важное обстоятельство - связь между динамическим выбором, сделанным системой в результате бифукации и нарушением симметрии. Появляющиеся в результате бифукации решения проявляются в виде иной внутренней дифференциации между различными частями системы или между системой и ее окружением. Дальнейшие рассуждения на эту тему могли бы привести нас к понятиям структурно-устойчивых и структурно-неустойчивых систем и условий их реализации, но это уже далеко выходит за рамки нашего исследования. Поэтому завершим этот раздел рассмотрением еще одной плодотворной попытки соединить двойственные понятия в одной модели, предложенной французским математиком Мандельбротом (Mandelbrot 1981, Пайтген 1993). Изучая состояние устойчивости, мы указывали на наличие состояний, - аттракторов, к которым стремится вернуться система, несмотря на воздействие флюктуаций и внешних воздействий. Известно (Николис 1990), что в математических моделях, размерность множества, представляющего аттрактор всегда меньше размерности самого фазового пространства и в трехмерном пространстве аттракторы, как правило, представлены точками, замкнутыми кривыми или ограниченными двухмерными поверхностями. Вопрос, на который, по существу, положительно ответил Мандельброт, заключается в следующем: возможны ли в трехмерном фазовом пространстве аттракторы промежуточного типа, лежащие между двойственными типами: точка - прямая, прямая - поверхность, поверхность- объем. Такие объекты, если они существуют, не будут ни точками, ни кривыми, ни поверхностями, ни вообще топологическим многообразием. Мандельброт дал им специальное название - фракталы. Простейший пример фрактальной структуры - множество Кантора ("пыль" Кантора). Оно появляется при ответе на вопрос - существует ли множество, промежуточное между множеством (типа множества натуральных чисел) и непрерывным континуумом ( типа совокупности точек на прямой). Ответ будет положительным. Рассмотрим отрезок [0,1]. Разделим его на три равные части и выбросим средний интервал. В каждом из двух оставшихся отрезков, которые мы тоже разделим на три равные части, снова выбросим средний интервал и т.д. В пределе мы получим несчетное множество изолированных точек. Это множество не имеет собственной длины (множество меры нуль), поскольку длина его дополнения до отрезка [0,1] равна единице:

1/3 + 2/9 + 4/27 + 5/81 + ... = 1

Но размерность (d) этого множества не равна нулю. Опуская доказательство, приведем сразу результат d_{кантора} »0,63. Таким образом в этом смысле множество Кантора промежуточное между точкой (d=0) и линией (d=1) т.е. оно является фракталом. С подобными множествами связывается появление так называемых странных аттракторов, являющихся естественными моделями хаотического поведения. Изучение странных аттракторов в хаотической динамике приводит к выводу, что в диссипативных системах с многими переменными возможно замечательное проявление двойственности: в таких системах возможно существование хаотического и регулярного поведения не только по отдельности, но и одновременно.

9. Двойственность и золотое сечение.

Простейшим примером проявления "золотого сечения" является задача о делении отрезка в крайнем и среднем отношении. Пусть имеется отрезок АВ, разделенный на две произвольные части точкой С, так что АС больше СВ. Требуется найти такое положение точки С, чтобы целое АВ относилось к большей части АС, также как большая часть относилась к меньшей, то есть необходимо выполнение соотношения АВ/АС = АС/СВ. В результате несложных преобразований можно получить уравнение х² - х - 1 = 0, положительным корнем которого и является искомое отношение a = 1,6180… (Шевелев, 1990).Это удивительное число, названное "золотой" пропорцией или сечением проявляется повсюду: в природе, в творениях человеческих рук, где речь идет о наиболее пропорциональном, гармоничном сочетании частей, входящих в целое. В другой интерпретации золотое сечение является пределом ряда a = lim Z_n+1/Z_n, где целые числа Z_n - задаются рекуррентным соотношением:

Z_n = Z_n-1 + Z_n-2.

Этот ряд называется последовательностью Фибоначчи и его первые члены имеют вид: 1, 1, 2, 3, 5, 8, 13, 21, ….

Можно переписать золотую пропорцию в виде a/b = a + b/a, где a>b. При такой записи видно, что есть две величины a и b, связанные отношением композиции a + b и отношением порядка а>b. Требуется найти такую структурную точку внутри непрерывной цепи, которая, не нарушая отношение порядка, обеспечивала бы "равновесие" четырех частей попарно связанных отношением порядка a+b>a, и a>b и композиции a+b/a и a/b. Число a = 1,6180 - единственное число, для которого a _{- 1} = a - 1 - 0,618…, то есть a - единственное число "сшивающее" два двойственных пространства: линейное, задаваемое функцией y=x-1 и гиперболическое у* = 1/х. Числа Фибоначчи фигурируют в давно известных в биологии законах филлотаксиса. Согласно им при многих случаях симметричного формообразования биологических объектов в числовых характеристиках их конфигураций реализуются пары фибоначчивых чисел из двойственных друг другу последовательностей (парастихной и ортостихной; Петухов, 1981) Z_n-1/Z_n и Z_n+2 /Z_n. Поучительный пример связи двойственности и золотого сечения предоставляет изучение цикла Карно. Известно, что тепловые и холодильные машины двойственны друг другу, они переходят друг в друга при обращениях идеального цикла Карно. Если мы зададимся задачей получения максимального значения к.п.д. (коэффициента полезного действия) для холодильной и тепловой машины одновременно, то окажется, что он равен a-1 = 0,6180. (Попков, 2000).

10. Двойственность. Материя и сознание.

До сих пор мы рассматривали двойственность так сказать с "божественной" точки зрения, совершенно игнорируя тот факт, что мы сами и наше сознание с его мыслями и чувствами является частью потока жизни и следовательно можно утверждать, что двойственность является неотъемлемой частью этого процесса. Появление квантовой теории показало, что наблюдение природы содержит неразрывную связь между наблюдателем и наблюдаемым. Индивидуализированное состояние мозга содержит таким образом объективный, внеиндивидуализированный уровень. Этот дуализм между объективным и субъективным указывает, что существует глубокое соответствие между материей и сознанием, что сознание и материя могут рассматриваться как два аспекта единого целого. Как существует неустраненная связь в квантовой теории между наблюдателем и наблюдаемым, также существует неустраненная связь между мыслями тех, кто мыслит. Акт мышления изменяет мыслящего. Мыслящий есть мысль; мысль порождает мыслящего, который в свою очередь рождает снова мысль. Кандел (Kandel, 1979) предложил модель двух взаимодействующих нейронных сетей находящихся в непрерывном танце друг с другом, который изменяет и устанавливает их обе. Мозг и сознание существуют как фонтан, который живет, пока есть поток воды его образующий. Можно рассмотреть следующую гипотезу. Неодушевленная, (точнее говоря немыслящая материя), рассматривается как "гибкий", изменяющийся каркас, (скелетная форма), которая связана отношением порядка. Отношение порядка в этой пространственно-топологической оболочке задается временем, текущим из прошлого в будущее. Эта действительность погружена в сознание, которое возбуждает и воздействует на нее. "Я - объект" как осознание "здесь и теперь" сознает свою принадлежность к опыту, который конструируется внутренней отнесенностью к миру реальности и миру идей. Но, "я-объект", конституированный таким образом. находится в мире реальности и проявляет себя как организм, требующий внедрение идей, чтобы закрепить свой статус в мире реальности" (Уайтхэд, 1990). Мысль не связана отношением порядка, она скользит из прошлого в настоящее и даже будущее в отличие от реальности не является для нее непреодолимым препятствием: за счет знания человек во многих случаях может с известной точностью предсказывать будущее.

Само тело и мозг также являются материальной "топологической" субстанцией и погружены в сознание; мы ощущаем себя прежде всего как сознание, как "Я", в которое погружена вся Вселенная. "Человек - это целый мир представлений, погребенных в ночи "Я" (Гегель, 1999). Существуют три группы композиционных отношений сознания к действительности: а) выделение себя из самого себя; б) выделение себя из материи, не обладающей мышлением; в) выделение себя из мыслящей материи, то есть из себе подобных, других людей. Мы уже отмечали вслед за Гегелем, что человек удваивает любое явление, ломая его надвое. Одновременно, только человек удваивает себя таким образом, что он есть всеобщее для всеобщего" (Гегель, 1999). Пример: животное, как таковое нельзя показать, а всегда можно показать конкретное животное, то есть животного как такового не существует - оно всеобщее. Но свойство быть животным, принадлежать роду как всеобщему, - это свойство порожденное человеческим умом; для животного нет всеобщего, для него всегда есть лишь единичное. Итак, если мир погружен в сознание, порождая человека как всеобщее, то разум рождает всеобщее для познания мира, раздваивая его при этом на парные категории с общим названием активность - сопротивление (сила - проявление, причина - следствие и т.п.) и этот мир, преобразованный мыслью, также погружается в сознание.

"Обращение "сути" и явления - особый закон универсума" и человек есть одна из возможных реализаций этого закона. Такое обращение сути и явления меняет взгляд на человека в принципе" ( Лефевр, 1991). Он приводит результаты любопытного эксперимента. Группе испытуемых выдавалось несколько десятков обыкновенных фасолин и предлагалось отсортировать их по произвольному (внутреннему для каждого) критерию на хорошие и плохие. Результат, усредненный по группе, был довольно неожиданным: "хорошие" фасолины относились к "плохим" в золотой пропорции (62% против 38%). На наш взгляд это проявление двойственности в смысле указанном выше. В самом деле человек в условиях неопределенного критерия рассматривает пару хорошее - плохое, как целое, в котором, в силу уже моральных установок хорошее должно быть больше плохого; - но насколько больше - это уже диктует "механизм" двойственности. заложенный в золотом сечении.

Лефевр (1978) предложил формализованный, алгебраический способ анализа взаимодействия познающего субъекта с действительностью, включающую в себя и других людей. Используя этот подход рассмотрим так называемый основной вопрос философии о соотношении материи и сознания. Существует две группы философских учений: идеалистическое (Х₁), материалистическое ( Х₂ ). Тогда в алгебраической записи любой объект действительности Т можно записать представленным в сознании человека картинкой Q с различных позиций: Q₁ = T + TX₁ + TX₂ - это дуализм, целостной картины нет. (ТХ₁ читается как Т с позиции Х₁). Q₂ = (T + TX₁ + TX₂) X₁ - целостная картина создана средствами идеалистического подхода. Q₃=(T+TX₁+ TX₂)X₂ - целостная картина создана с позиции материализма. На наш взгляд необходим новый подход, который можно записать как: Q₄=(T+TX₁+TX₂)X₁+(T+TX₁+TX2) X2 - целостная картина создается на основе новой позиции синтеза двойственной природы объекта. Обозначив TX₁=T₁* и TX₂ = T₂*, можно представить Q₄ в виде Q₄=T₁*+T₂*X₁+T₂*+T₁*X₂, T₁*+T₂* - отношение композиции; T₂*X₁ + T₁*X₂ - отношение порядка. В работе (Лефевр, 1978) вводится полезное понятие "экран сознания, - аналог отклика (реакции) сознания на воздействие действительности. Экран сознания действует по принципу - "я думаю, что ты думаешь…", где под "ты" понимается либо немыслящая субстанция, и корректировка (самосогласование, подстройка) происходит в вибрационном режиме взаимодействия себя с самим собой (или точнее первоначальных представлений с вновь возникающим); либо в более сложном случае под "ты" понимается другой мыслящий объект. Подобный прием использовал Богданова (1907), введя подстановку, которая исходит из признания существования психики других людей или социальности познания. "Когда под такие-то данные высказывания других людей я подставляю такие-то данные чувства и мысли, то гипотетично здесь только данное содержание подготовляемого; оно нередко и бывает ошибочным, я могу не понять других людей. Но сама подстановка - отнюдь не гипотеза, а конститутивный признак познания... Подстановка не представляет из себя ни в коем случае выхода за пределы возможного опыта. Ее правильность проверяется практикой "Используя подстановку, Богданов (1907) разбирает весьма тонкий вопрос о дуализме последовательного (каузального) познания действительности и параллельного (одновременного) схватывания ее как целого. Эта проблема в более полном, правда, аспекте до сих пор до конца не разработана, но все в большей мере приковывает внимание исследователей. Пит (Peat, 1987) приводит диаграмму, предложенную известным физиком В.Паули (сформулировавшим, кстати, принцип запрета: два электрона могут находиться в одном квантовом состоянии, только имея противоположные спины ).

Все события текут и раскрывают себя (unfold out) в независимых от времени картинах (patterns) одновременности скорее, чем последовательность казуальных связей в линейном времени." Им был предложен подход: рассматривать в целом порядок материи и порядок мышления и в этом случае определять: если эти два порядка несовместимы, то речь идет о дуализме; или если они лежат в пределах общего спектра. Если мышление и материю можно понимать как проявление общего порядка, тогда будет полезно мыслить их оба не как отдельные субстанции, а скорее как неразделимые проявления одного индивидуального целого. Пит не раскрывает, что он вкладывает в понятие "порядок", но мы можем это сделать, если вспомним модель Крона к ее топологическим "скелетом" (действительность); погруженным в изменяющуюся плазму - "сознание".

11. Двойственность. Контуры теории.

Определения.

Среди редких штрихов уже приведенных фактов и суждений все более явственно проступают контуры теории, которая с большим основанием может претендовать на всеобщность, поскольку как и тектология не привязана к конкретной науке, а наоборот, из всех наук может черпать все новые и новые факты в подтверждении необходимости своего существования. Основа плодотворной теории заключается в том, чтобы начинать с постулатов, которых можно было бы придерживаться при рассмотрении любого вопроса, но прежде чем попытаться сделать это необходимо все-таки вернуться к вопросу дефиниций и вычленить понятие двойственность (коль скоро мы решили не вводить нового термина) из родственных ему терминов с характерными приставками "ди", "ду", "диа", "против" и др. Дихотомия согласно статье данной в философском словаре (Философский словарь 2000); проводится по логической формуле исключенного третьего и делит некоторое множество ровно на два класса объектов, тогда как двойственность представляет собой единое, в различных условиях проявляющее то или иное свойство, принадлежащее к одной из ветвей парной категории. Диада (греч. - двоица) - термин для обозначения принципа неопределенности, множества в противоположность монаде (единице). Диада - оппозиция монаде. Входит в "четверку" у пифагорейцев, которая как мы видели, может характеризовать двойственность. Дуализм - несводимость двух начал, чаще всего имея в виду материальное и идеальное. Таким образом, двойственность существенно шире дуализма, признавая с самого начала (ad ovo) естественным наличие единого, выраженного в двойной мере понятий. Авенариус понимая, что существует разница между дуализмом и двойственностью, выразил это категорической фразой "Diese Dualitat ist keine Dualismus" - Эта двойственность не есть дуализм. (Цит. - Богданов, 1907 ).

Бинарная оппозиция - термин (Сороко, 1984) наиболее близкий к двойственности поскольку указывает на двойное существование, но часть термина "оппозиция" искажает смысл, уводит его от двойственности. Для наглядности приведем пример: рисунок, нанесенный на ткань - совершенно естественно, что его можно считать иллюстрацией двойственности; но бинарной оппозицией назвать его не поворачивается язык.

Наиболее сложным оказывается взаимоотношение двойственности с противоположностью и противоречием. Движение противоположности и противоречия наиболее полно разработано в диалектике Гегеля.

Двойственность,противоположность, противоречие

Как только закон мышления выступает как суждение, то он различает субъект и предикат, он содержит в себе различие. Различие по Гегелю развивается в троякой, с каждым шагом все глубже проникающей форме. Первая состоит во внешнем различии - есть разность. Вторая - во внутреннем или имманентном различии, заключающемся в том, что нечто отличается от другого, которое есть его другое. Эта форма различия называется противоположностью. И наконец, третья форма состоит в различении себя от самого себя - это противоречие. Из природы противоположности ясно, что каждая из двух сторон (нечто и его другое и наоборот) необходимо соответственна с другой, связана с ней, так что полагает и требует также небытия другой стороны, каждая сторона как полагает так и отрицает другую сторону, относится к ней как положительно, так и отрицательно, и потому составляет целую противоположность, и, что одно и то же, противоположна самой себе. В этой противоположности самому себе состоит сущность противоречия (Фишер 1933).

Без противоречия, этого единства противоположных определений в сущности вещей, нет никакого возникновения, изменения, жизни, развития. А где же в этом потоке жизни место двойственности, какова ее роль в структуре взаимозависимых переходов и единства противоположностей?

Каждая из противоположных сторон противоречия, составляющих нечто, скажем,- А, вызвана к жизни его не-А, которое есть его другое. Противоречие внутри А формируется из-за существования противоположности между становящимся в действительности "А" и противодействующем этому изменению в действительном мире воздействии на "А" его "не-А". Обозначим это его другое через "А" со звездочкой или "А*". Поскольку для "А*" его другим является "А" , то, соответственно, стороны противоположности меняются местами; если в сущности "А" противоречие образовано противодействием противоположного ему "А*" , то это изменение представляется в виде становления "А*", вызывающее соответствующее изменение (реакцию) "А" и так далее, - продолжая до бесконечности эту пульсацию жизни. Таким образом, внутреннее, имманентное противоречие некой сущности оказывается связанным с внешней противоположностью окружающей ее действительности, причем связь носит особый, двойственный характер, описанный выше. Понятно, что такое понимание проявления двойственности через взаимопереходы и взаимопереплетение имеет чрезвычайно важное практическое значение для деятельности человека. Планируя свои действия, готовясь ввести в этот мир новую сущность, мы должны ясно себе представлять, что ее появление вызовет реакцию отклика, противодействующей изменениям. Поскольку мир, в котором происходит становление бесконечно многообразен, то и проявление этих откликов и отклики новой сущности в соответствии с двойственным характером взаимодействия, практически непредсказуемы. И только об очень явных последствиях удается что-то сказать более или менее определенное, но всегда с известной долей ошибки. Поэтому силы ума человека должны быть направлены не на подсчет результата, который зачастую оказывается мифическим, а на формирование, продумывание тех мер, которые бы обеспечивали адекватную реакцию на бесконечную цепь изменений, развития, пульсацию жизни. Отсюда понятна вся бессмысленность и пагубность централизованных решений, жестких планов и т.д., но это уже тема для отдельного разговора.

Двойственность "отрицания отрицания"

Диалектическое "отрицание отрицания" означает движение, развитие. Это двойное отрицание заключает в себе проблему становления. Каким образом в этом сложном, меняющемся мире возникает, становится новое? Как оно связано с тем, что есть, при каких условиях новое получает право на жизнь и как оно с неумолимостью становится старым? Почему развитие имеет циклическую, пульсирующую природу? Вот те главные вопросы, на которые по существу делается попытка дать ответ в рамках концепции, или как еще называют закона "отрицания отрицания". Существует множество формулировок и толкований этого закона. Но как бы не отличались они по форме и полноте описания, в них можно выделить два основных момента, без которых нельзя понять суть "отрицания отрицания". Первый из них обращает внимание на процессный характер "отрицания отрицания". Утверждается, к примеру, что диалектическое отрицание отрицания включает в себя триединый процесс: деструкции (разрушения, преодоления, изживания) прежнего, кумуляции (его частичного сохранения, преемственности, трансляции) и конструкции (формирование, созидание нового) (Введение,1989) .

Второй аспект связан с признанием необходимости для развертывания процесса развития именно двойного отрицания. Диалектическое отрицание или "снятие" противоположностей обеспечивает сохранение некоего остатка, - новой сущности, которая либо утверждает себя через последующие циклы "снятия", либо, не имея возможности для развития, - погибает. Но даже ее гибель не проходит бесследно, отрицание гибели, отрицание отрицания и здесь проявляет свою созидающую роль. Факт зарождения и гибели не остается незамеченным, он оставляет свои изменения в мире и создает предпосылки для рождения других сущностей.

Знание двойственного механизма взаимодействия противоположностей может пролить дополнительный свет на тонкую структуру взаимоотношений противоположностей в диалектическом отрицании. Постараемся это сделать, сформулировав несколько основополагающих утверждений

Утверждение 1. Способностью к развитию (креативностью) обладают открытые системы, обменивающиеся потоками энергии, материи, информации с окружающей действительностью. Такие системы, как мы уже отмечали, называют неравновесными или системами динамического равновесия. Их особенностью является постоянное нарушение и возобновление равновесия за счет единства двух процессов - ассимиляции (усвоения) и дессимиляции (разложения, выделения).

Утверждение 2. Чем более замкнута система, тем меньше возможностей она имеет для развития. Ограничение потоков энергии, материалов, информации ведет к деградации системы и ее последующей гибели. Одна из гипотез, объясняющих причину смерти живого, основана на том, что клетки теряют постепенно способность к обмену из-за нарастания ошибок при их репликации.

Один из сценариев деградации - это вырождение системы. Вместо спирального развития происходит движение по кругу, не вносящее ничего нового, не имеющее становления. Примером могут служить многие изолированные системы, когда мы можем пренебречь рассеиванием (диссипацией) энергии. На этом допущении основаны многие важные прикладные расчетные приемы.

Утверждение 3. Процесс "отрицания отрицания" включает в себя четыре фазы: первое отрицание, развитие, второе отрицание или "отрицание - звездочка" и следующая фаза вновь развитие, но теперь уже "развитие - звездочка". Развитие - звездочка есть снятие от действия двойного отрицания. Рассмотрим это подробней. Сразу же отметим, что первое отрицание и развитие, как и второе отрицание и развитие со "звездочками" представляют из себя единые циклы, которые невозможно разделить во времени. Всякое рождение нового - это момент развития и одновременно отрицания старого. Но тем не менее такое членение имеет смысл, так как подводит нас к изучению еще одной важной проблемы, неразрывно связанной с развитием. Речь идет о проблеме выбора. Развитие невозможно без выбора между различными путями развития. Понятно, что выбор обусловлен открытостью системы, в замкнутой системе выбор ограничен или невозможен: чем более открыта система, тем больше у нее возможностей для выбора. Выбор осуществляется на основе внутреннего критерия, присущего данной системе. В качестве критерия часто действует принцип "минимакса", т. е. достижение максимума результатов при минимуме затрат. Существенными являются три обстоятельства. Первое - это то, что выбор одного варианта развития исключает или, по крайней мере, сильно ограничивает другие варианты. Второе - выбор хотя и осуществляется при развитии непрерывно, но имеет особую важность в некоторых узловых точках, образующих по Гегелю "узловую линию". В теории неравновесных систем эти точки ввиду их важности получили специальное название - "точки бифуркации" (Николис, 1990).

И наконец, чем богаче возможности выбора и, соответственно, условия для развития, тем более неопределенным является возможный результат этого выбора. Это происходит потому, что все остальные , невостребованные пути развития не исчезают, они формируют для вновь рожденной сущности его другое или тот фон, те условия, в которых осуществляется фаза последующего развития и чем богаче и многообразней картина их взаимодействия, тем менее определенным будет результат выбора.

Итак , первая фаза развития - это выбор, отрицание из "своего другого" , - внешней противоположности всех путей развития, кроме одного. Это становление, появление нового в условиях неопределенности, в сильно неравновесной области. Эта неравновесность есть одновременно и причина и следствие появления нового. Далее следует фаза развития, новое утверждает себя. Но при этом внешние к становящемуся противоположности тоже претерпевают процесс изменения, превращаясь в иные "его другие", из которых вновь необходимо делать выбор - второе отрицание, или отрицание отрицания. При этом возможны два исхода, - либо следующая фаза развития (развитие со звездочкой в изменившихся условиях), либо гибель (понимаемая как предпосылка для рождения иного нового).

Таков, на наш взгляд, "механизм" самовозобновления движения материи на основе диалектического отрицания отрицания. Это единство спокойного (ламинарного) , в значительной мере предсказуемого и неопределенного, вихревого, плохо предсказуемого этапов развития. Существование некоторой неопределенности является неотъемлемым атрибутом развивающейся системы, тем резервуаром, откуда черпаются все новые возможности для развития. Наличие неопределенности есть одновременно и плата за развитие и взнос в фонд развития.

Исходя из принципа единства мира можно предположить существование принципа неопределенности для развивающихся макросистем: "Чем больше мы локализуем движение системы, ограничивая возможности выбора, тем меньше мы оставляем возможности системе для саморазвития, саморегуляции".

Стремясь к развитию, мы должны смириться с наличием неопределенности и отказаться от мысли, что процесс развития может подчиняться строгим детерминистским законам. Для познания таких систем необходимо двойственное детерминизму вероятностное описание.

В свете этого мы должны по-новому взглянуть на проблему соотношения стихийного и сознательного, случайного и необходимого. Старое, полупренебрежительное отношение к левым частям этих дихотомий (стихийности, случайности) как к чему-то второсортному, существующему только благодаря тому, что мы не до конца познали действительность, должно смениться уважением и пониманием той равноправной роли, которую они наряду с необходимостью и сознательностью занимают в изменяющемся и развивающемся мире.

Динамический принцип двойственности

Завершая наш краткий обзор проявлений двойственности в различных областях человеческого знания, сделаем попытку сформулировать обобщающий принцип двойственности и следствия из него. Итак, принцип двойственности:

В развивающейся, взаимозависимой действительности становление новой сущности вызывает такое изменение в ее внешнем окружении, которое порождает внутреннее противоречие этой сущности, приводящее к изменению внешней противоположности и появлению внутренних противоречий в сущностях, образующих это окружение. Таким образом, образуется качественно новое окружение, по отношению к которому первоначальная сущность является внешней противоположностью и цикл развития возобновляется.

Следствие 1.

"Вследствие бесконечного многообразия, окружающего данную сущность мира, внутренние противоречия, раскрывающие себя во внешних противоположностях, представляются в виде непредсказуемо появляющихся новых сущностей, каждая из которых может служить точкой процесса развития согласно принципа двойственности".

Следствие 2.

"Чем жестче система введения в действительный мир новых сущностей, тем быстрее и резче проявляются противоречия и при отсутствии необходимого механизма коррекции, противоречия нарастают и приводят к кризису системы".

Следствие 3.

"Наибольшей приспособляемостью и способностью к саморегуляции и самоорганизации обладают системы, представляющие из себя многомерные "проводящие" сети, погруженные в изменяющуюся, пульсирующую среду". 12.

Двойственность. Алгоритм поиска нового.

В этом разделе в соответствии с логикой изложения постараемся привести некоторую типичную процедуру, играющую роль поисковой сети или каркаса - средства, которое можно погружать в любую среду для ее изучения. На возможность сформулировать такие пошаговые правила (алгоритм) указывают повторяющиеся признаки проявления двойственности в природе и человеческом знании. Кроме этого выше мы указывали на эвристичность и методологическую важность применения принципа двойственности в практической и научной деятельности и поэтому, наше исследование было бы неполным, если бы мы не попытались дать воспроизводимый любым исследователем механизм использования основных результатов, изложенных в этой работе. Разумеется, эта попытка является лишь грубым отображением более глубоких и тонких методов, о которых мы уже упоминали, и которые развиваются и могут быть развиты в дальнейшем. Но тем не менее даже в этом упрощенном виде, приведенный алгоритм может сыграть важную роль. Доказательством, к примеру, могут служить результаты работы (Попков, 2000), где авторам, используя двойственный подход удалось получить новые результаты в хорошо известном и давно изученном цикле Карно.

Для ясности и четкости восприятия мы изложили алгоритм в императивном стиле, что, конечно, не означает, что исследование будет столь же стремительно продвигаться как это изложено в процедуре. Безусловно, на каждом этапе потребуются длительные размышления, сопоставления, в том числе с вышеприведенными моделями, чтение и изучение специальной литературы и т.п., - все то, что сопутствует работе исследователя.

Итак, алгоритм применения двойственности при рассмотрении любого процесса (а реальность - это всегда процесс).

Шаг 1. Ищи двойственную данному явлению систему. Помни о том, что она всегда существует - это объективное свойство реальности. Если не удается с ходу выявить двойственную систему раздвои явление, разломи его на две части. Это раздвоение неоднозначно, но оно всегда возможно. Логика раздвоения диктуется предметом и целью исследования, а также возможностями использовать правила следующих шагов.

Шаг 2. Выдели части, соответствующие двум характерным ветвям двойственности: отношению порядка и отношению композиции. Помни о том, что для отношения порядка (структурная часть двойственности) характерно дискретное описание, отношение композиции характеризуется непрерывной функциональной связью.

Шаг 3. Ограничь вначале рассмотрения проблемы стационарным линейным случаем.

Шаг 4. Выяви линейные приближения отношения композиции, найди четверку взаимно - попарно связанных параметров. Характерный признак - один из них в какой-то из пар должен обладать особым характером.

Шаг 5. Ищи закон композиции между этими четырьмя параметрами (или четыре возможности описания). Постарайся построить модель качественную или количественную (в каждом случае попытайся записать математическую зависимость, типа X+Y* = F (X*+Y)

Шаг 6. Изучи внимательно отношение порядка. Ищи способы описания перехода одной структуры в другую. Характерным признаком такой возможности является наличие инвариантов.

Шаг 7. Ищи инварианты системы. Выяви те преобразования структуры, которым соответствуют инварианты.

Шаг 8. При поиске инвариантов, прежде всего, обрати внимание на различные сочетания параметров из пункта 5.

Шаг 9. Совмести оба описания пунктов 4 и 6 . Одним из отправных пунктов поиска такого совмещения - особый характер одного из параметров, порой указывающий на возможность перехода к двойственному описанию. В результате применения двойственного описания получи новые результаты.

Шаг 10. Ищи двойственную "невидимую" систему. Для этого проведи операцию типа "обращение стрелок". При этом исходи из того, что в простом приближении: f (a, b), f*(a*, b*), где параметры, помеченные знаком (*) двойственны параметрам без этого знака и принадлежат соответственно обратному и прямому пространствам. В результате операции обращения получи новый результат.

Шаг 3*. Если в пункте 2 не удается выделить двойственную систему примени правило: "Структура (порядок) порождает функцию (композицию); функция порождает структуру". Для срабатывания этого правила необходим пункт 4*.

Шаг 4*. Введи неоднородности (флюктуации) в закон композиции, что означает переход к более сложной нелинейной модели. Нелинейность породит структуру, исследуй ее на устойчивость и симметрию (симметрия всегда указывает на существование инвариантных свойств).

Шаг 5*. Далее следуй в соответствии с логикой алгоритма, задаваемого пунктами 4-10. Именно, с логикой, поскольку простое исследование уже невозможно; число параметров будет уже не четыре, а больше, но, как правило кратно двум (4, 6, 8...) Закон порядка трудно будет отдельно выделить, он будет "вплетен" в отношение композиции и т.д.; в общем, здесь уже слишком многое зависит от конкретного исследования и подготовкой исследователя, чтобы давать должное детальное описание.

Итак, подведен итог изложенному. В предложенном алгоритме просматриваются следы пресловутого "единства" борьбы противоположностей, но если бы мы не сделали принципиальный шаг к переходу к двойственному описанию с сопутствующему ему выявлением двойственных ветвей, то мы бы не продвинулись так далеко по пути понимания механизма действия взаимных переходов и взаимодействия двойственных частей, особенно ее "невидимой" части. В этом состоит суть и прелесть развиваемого нами направления, которое наряду с теоретическими изысками (как мы видели, весьма элегантными и сложными) позволяет во многих более простых случаях получать нетривиальные результаты, рассматривая простые, "на пальцах" соотношения двойственности. В этом смысле принцип двойственности вполне может претендовать на роль всеобщего организационного принципа, созвучного тектологии А. Богданова.

13. Двойственность. Вместо заключения.

"Порочный дуализм всегда обусловлен тем, что абстракция принимается за окончательный конкретный факт. Вселенная двойственна потому, что она одновременно является и проходящей и вечной; каждый завершенный элемент реальности обладает и физической и духовной сторонами; каждая актуальность требует некоторой абстрактной характеристики; каждое событие объединяет в себе формальную непосредственность и объективную плановость"

(Уайтхед А. "Процесс и реальность")

Утверждают, что XXI век - это век Водолея, который характерен распространением интеллектуальной энергии, усилением исследовательской сущности человека, преодолением сложившихся предрассудков, ломкой привычных представлений и генерированием новых идей. С этой точки зрения теория двойственности, общие черты, которой обозначены в представленной работе, вполне соответствует духу наступившего нового тысячелетия. Сразу оговоримся, что эта тенденция поиска особых сохраняющихся отношений, имеющих универсальный характер, прилагаемых к анализу массы кажущихся совершенно разнородных явлений возникла уже давно, в конце XIX века с появлением открытий в области термодинамики и электромагнетизма. ХХ век только усилил эту ориентацию, чему способствовали новые открытия всеобъемлющего характера: создание теории относительности и квантовой механики, развитие генетики и кибернетики. Все это способствовало преодолению гипнотического влияния механицизма, раскрытию возможности для развития новых идей во многих областях научной мысли и практической деятельности.

Мы уверены, что эта тенденция будет только усиливаться, причем в двух направлениях. Во-первых, изменится сам характер научных исследований. Известно, что современная наука разъединена на локальные, дисциплинарные "земли" -, в каждой из которых, изучая в общем-то в конечном счете одно и то же - Вселенную, говорят на совершенно разных, специальных языках. Преодоление этой "кастовости", поиск единых, универсальных принципов, на которых могут нанизываться композиции специальных наук - это благодарная задача, достойная любого исследователя. Во-вторых, еще более важным является формирование нового стиля мышления у новых поколений и не только исследователей. Даже в средних школах учащиеся перегружены, изучая по много раз и в разном изложении факты, количество которых неустанно растет и уже сейчас превышает разумные пределы. То же самое происходит и в вузах и специальных учебных заведениях. Вместо наборов слабо связанных фактов надо сосредоточить внимание на общих принципах организации материи, - тогда факты любой науки легко лягут в ячейки универсальной сети принципов. Сильнейший прорыв в этом направлении был сделан А. Богдановым в его тектологии, которую необходимо также доводить до рецептов практического применения, пригодных для любого мало-мальски подготовленного ума.

Надеемся, что дальнейшее развитие двойственного подхода будет также способствовать решение этой двуединой задачи. Алгоритм поиска нового основанный на всеобщем принципе двойственности представляет как раз малый, но наш взгляд, весьма своевременный шаг в нужном направлении.

Библиография.

1. Беллюстин В. Как постепенно дошли люди до настоящей арифметики. М.-Пг. - 1923
2. Богданов А.А. Эмпириомонизм. Статьи по философии. Книга 2. Санкт-Петербург. издательство С. Дороватовского и А. Чарушникова. 1907.
3. Богданов А.А. Тектология. Всеобщая организационная наука. Книга 1.2. Москва. экономика. 1989.
4. Бриллюэн Л. Термодинамика - кибернетика - жизнь // Кибернетика. Современное состояние. М. 1980.
5. Букур И.. Делану А. Введение в теорию категорий. М. Мир. 1972. Введение в философию. М. Политиздат. ч.2. 1999.
6. Гамалей Ю.В. Таксономическая и экологическая специфичность структур и функций растений // Ботанический журнал. 1999. Т. 84. №6.
7. Гегель Г.В.Ф. Наука логики. М. - Мысль. - 1998.
8. Глаголев Н.А. Проективная геометрия. Госиздат. М. 1963.
9. Градштейн И.С. Прямая и обратная теоремы. М. Наука.1973.
10. Инге-Вечтомов С.Г. Введение в молекулярную генетику. М. Высшая школа. 1983.
11. Карманов В.Г. Математическое программирование. М. Наука. 1986.
12. Киселев А.П. Геометрия. Учебник. 9 класс. средняя школа. Ч.1. Учпедгиз. 1958.
13. Колмогоров А.Н. Три подхода в определении понятия "количество информации" // Проблемы передачи информации. М. 1968. т. 1. Вып 1.
14. Крон Г. 1960. Диакоптика - решение сложных задач п частям..
15. Крон Г. Тензорный анализ сетей. М. Сов. Радио. 1978.
16. Кузнецов П.Г. Диалектическая логика. Препринт. 1988.
17. Лефевр В.А. Конфликтующие структуры. М. Советское радио. 1973.
18. Лефевр В.А. Формула человека. М . Прогресс. 1991.
19. Налимов В. Жизнь как язык // Наука и техника. №1. 1981.
20. Николис Г., Пригожин. Познание нового. Введение. М. Мир. 1990.
21. Пайтген Х.О., Рихтер П. Х.. Красота фракталов. М. Мир. 1993.
22. Паленко М.Ш., Шульгейфер Е.Г. Основы теории категорий. М. 1974
23. Петухов С.В. Биомеханика. бионика и симметрия. М. Наука. 1981.
24. Платон. Законы. М. - Мысль. - 1999.
25. Попков 2000. Щипицын Е.В. Цикл Карно и золотое сечение. Препринт.2000
26. Пригожин И.. Стенгерс И. Порядок из хаоса. М . - Прогресс. - 1986.
27. Рассел. 1999. История западной философии. М. - Мысль. - 1999.
28. Румер Ю.Б.. Рывкин М.Ш. Термодинамика. статистическая физика и кинетика. М. - Наука. - 1977.
29. Седов Е.А.. 1978. Языки науки и наука о языке // Химия и жизнь. №9. 1978.
30. Сороко. Структурная гармония систем. Минск. - Наука и техника 1984.
31. Уайтхед А.Н.. Избранные работы по философии. М . - Прогресс. - 1990 Фейнман Р. Характер физических законов. М.- Мир.- 1968
32. Фейнман Р.. Лейтон Р.. Сэндс М. Фейнмановские лекции по физике М.. Мир 1967
33. Философский энциклопедический словарь М. - ИНФРА-М. 2000
34. Фишер К. История новой философии Том 8. Гегель . 1933
35. Франк-Каменецкий М.Д. Самая главная молекула. М.. Наука. 1988
36. Шевелев И.Ш.. Марутаев М.А. Золотое сечение. М.. Стройиздат. 1990
37. Эткинс П. Порядок и беспорядок в природе. М.- Мир.- 1987
38. Bertalanffy L.von. Biophisik des Fliessgleichgewichtes. Braunschweig - Berlin. - 1922. 1953
39. Bohm D and Peat F.D. Science, Order, Creativity. New York, Bantam Books - 1987
40. Gegel G. Encyklopedie der Wisseschafte. Akademie, Verlag. - Berlin, 1975.
41. Kandel E. Small Systems of Neurons Scientific American 1979 No.9 (sept)
42. Kron G. Self-Organizing Dinamo Typo Automato The Matrix and Tensor Quorterly. Vol. XI. Desember, 1960.
43. Mandelbrot B. The Fractal Geometry of Nature. San Francisco - 1981.
44. Peat F.D. Synhronisity: the bridge between matter and mind. Toronto, Bantam Books - 1987
45. Zeleny M. Tektology General Systems: An Internatonal Journa. Vol. 14. 1988